Difference between revisions of "Random Number Generator"

Revision as of 11:04, 22 May 2019

This article goes into very technical detail. The information is presented with the assumption that the reader has at least basic knowledge of hexadecimal, bitwise operations, SNES memory, and/or SNES assembly.

The Random Number Generator or RNG in A Link to the Past is a weak algorithm used to generate numbers for events.

Source

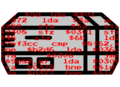
The RNG function is found in Bank0D of the game's code. This is how it appears in the MoN disassembly without comments:

; *$6BA71-$6BA7F LONG
GetRandomInt:
	LDA $2137
	LDA $213C : ADC $1A : ADC $0FA1 : STA $0FA1
	RTL

Explanation

Looking at each instruction separately, here is an explanation of the code:

LDA $2137 is simply reading a hardware register. LDA means "Load into Accumulator" for the address that follows. Address $2137 is a software latch. When this register is read, it also stores the value of the horizontal pixel counter into address $213C.

LDA $213C is reading the value latched read by the previous instruction.

ADC $1A adds with carry the value in the accumulator and the value in address $1A, which is a 1 byte counter that increments every frame the game does not lag, wrapping around to 0 after 255.

ADC $0FA1 takes that value and adds with carry the current value of $0FA1, which is a 1 byte storage for RNG values.

STA $0FA1 takes that final value and stores it in the RNG address. As such, this means all RNG values are based on the previous value generated.

Analysis

From a mathematical standpoint, this function is not a strong function, even if the fact that it can only generate 256 values is ignored. It is, however, unpredictable enough in real-time that it will seem random enough. Even in a TAS environment, the nature of the horizontal pixel counter makes generating a specific value difficult; however, an understanding of how the number is generated makes creating a different value or generation time trivial without losing even a single frame.

In essence, the use of the horizontal pixel counter means that, in general, more work for the CPU means the function is called later, and the RNG values generated are different. The use of the frame counter means that waiting 1 or more frames may generate a different value, even without intermediate RNG calls.

All these conditions present a problem with multiple values per frame. As a simple example, imagine there is an enemy that moves in a random direction when it's spawned, either up or down. If the sprite generates an even number, it will move up; for odd, it will move down. Let's say that Link enters the room walking by holding <, and the RNG generates the values $13, $F7, and $5A. In this instance, enemies A and B move down, while enemy C moves up. Now imagine that Link enters the room walking by holding <v. This provides the CPU slightly more work on that frame. Let's imagine it doesn't add a lag frame, but it does delay the first RNG call. Let's say it took 3 extra horizontal pixels for the first call. Nothing else changed this frame, so the work between each call is the same. Now the values are $16, $FA, and $5D. Now enemies A and B move up, while enemy C moves down. If we continue this example but imagine a change of only one variable (e.g. the RNG value is different, but the movement entering the room was the same), we'll notice that enemies A and B always move in the same direction, and enemy C always moves in the opposite direction of those 2. For a more random generation, the expected result is that every value is independent. From our understanding of the function, though, such a set of results is impossible.