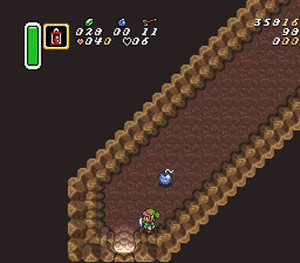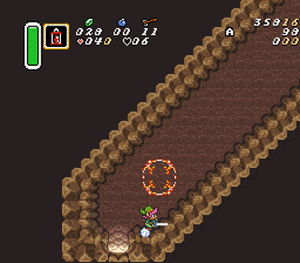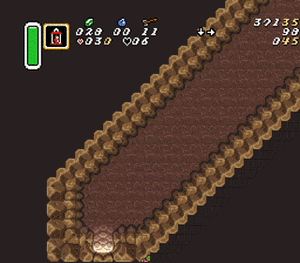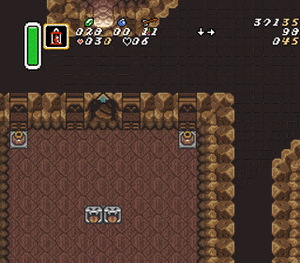
Bomb Clips
You can clip through a diagonal slope (both indoors and outdoors) by taking damage, and be damage boosted into the wall.
Requirements for bomb clips to work
- Link needs to be dashing on a slope.
- The damage source needs to be exactly perpendicular to the direction Link is facing, such that the damage boost happens in a cardinal direction into the wall.
- Link can only clip through walls with slope properties using this.
The general RTA technique
- Put down bomb at a specific coordinate.
- Put Link on a specific row/column of coordinates.
- Wait for the bomb to start blinking.
- Start your dash into the slope.
- Dash into the bomb explosion.
That last part is the essential part of making this RTA-viable. You don't have to be below the bomb explosion as it explodes. Instead you let it explode, and then dash into the explosion. In effect, the timing of the dash if "free". You have around half a second to start the dash. If you fail the clip, and aren't sure why, it's probably not due to mistiming the dash.
Problems
Since Link is required to get damaged in a cardinal way, you will need to hit the explosion on a specific pixel. This is part of the setup - put the bomb on a specific pixel, start the dash from a specific row/column of pixels. However, there is one more variable, and that is Subpixels.
Your subpixel before starting the dash matters just as much as your coordinate, since different subpixels means different paths through the slope. And you need to hit a specific pixel.
So some setups will require you to manipulate your subpixel before starting the dash. This is typically done by moving in a specific direction for only one frame. For example "swordbuffer one frame movement toward left/right before you start the dash".
Other setups will work the same for all subpixels, in which case only the coordinate matters.